Como se verá a continuación, la inductancia (mutua y autoinductacia) es una característica de los circuitos que depende de la geometría de los mismos. Sean dos circuitos arbitrarios descritos por las curva
γ1 y
γ2 por donde circulan corrientes
I1 y
I2, respectivamente. De ahora en más el subíndice 1 representa magnitudes correspondientes circuito 1 y análogamente para el circuito 2. En virtud de la Ley de Faraday se tiene

donde

es el campo eléctrico y

es el campo magnético en el circuito 1. Si ahora se toma el flujo a través del área encerrada
S1 por el circuito 1,

y usando el Teorema de Stokes para la integral del lado izquierdo se obtiene la fem
ε1 para el circuito 1:
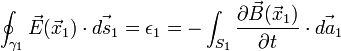
Es conveniente usar que

, donde
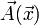
es el potencial vectorial para reescribir lo anterior como
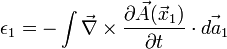
En este punto se debe hacer una simplificación: se supondrá que el circuito no cambia en el tiempo, con lo cual la derivada parcial puede salir fuera de la integral. Esto permite entonces aplicar nuevamente el Teorema de Stokes. Matemáticamente:

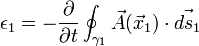
Dado que

en el gauge
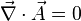
donde

es la densidad de corriente que genera el campo magnético
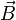
. En este caso la densidad de corriente corresponde a la del
circuito 2, por lo que

. En caso que la densidad de corriente corresponda a una curva y no a un volumen en el espacio es lícito reescribir el potencial vectorial como

. Luego, reemplazando esta última igualdad en la expresión anterior se tiene

Dado que se ha supuesto que los circuitos no se modifican en el tiempo sólo
I2 se ve afectada por la derivada temporal, con lo que
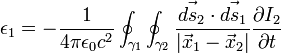
El anterior razonamiento se puede repetir para el circuito 2 dando como resultado
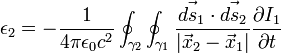
Claramente las constantes que acompañan a las derivadas temporales en ambos casos son coeficientes que sólo dependen de la geometría de los circuitos y además son iguales. Luego se llama
inductancia mutua,
M a dicha constante


 es el campo eléctrico y
es el campo eléctrico y  es el campo magnético en el circuito 1. Si ahora se toma el flujo a través del área encerrada S1 por el circuito 1,
es el campo magnético en el circuito 1. Si ahora se toma el flujo a través del área encerrada S1 por el circuito 1,
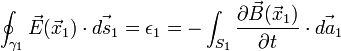
 , donde
, donde 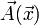 es el potencial vectorial para reescribir lo anterior como
es el potencial vectorial para reescribir lo anterior como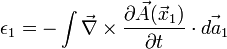

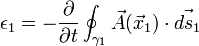
 en el gauge
en el gauge 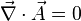 donde
donde  es la densidad de corriente que genera el campo magnético
es la densidad de corriente que genera el campo magnético 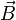 . En este caso la densidad de corriente corresponde a la del
. En este caso la densidad de corriente corresponde a la del  . En caso que la densidad de corriente corresponda a una curva y no a un volumen en el espacio es lícito reescribir el potencial vectorial como
. En caso que la densidad de corriente corresponda a una curva y no a un volumen en el espacio es lícito reescribir el potencial vectorial como  . Luego, reemplazando esta última igualdad en la expresión anterior se tiene
. Luego, reemplazando esta última igualdad en la expresión anterior se tiene
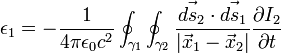
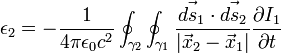

No hay comentarios:
Publicar un comentario