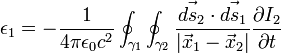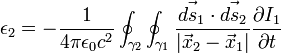FISICA II

jueves, 11 de noviembre de 2010

INDUCTANCIA MAGNETICA

La inductancia es el campo magnético que crea una corriente eléctrica al pasar a través de una bobina de hilo conductor enrollado alrededor de la misma que conforma un inductor. Un inductor puede utilizarse para diferenciar señales cambiantes rápidas o lentas. Al utilizar un inductor con un condensador, la tensión del inductor alcanza su valor máximo a una frecuencia dependiente de la capacitancia y de la inductancia.

La inductancia depende de las características físicas del conductor y de la longitud del mismo. Si se enrolla un conductor, la inductancia aumenta. Con muchas espiras se tendrá más inductancia que con pocas. Si a esto añadimos un núcleo de ferrita, aumentaremos considerablemente la inductancia.

Existen fenómenos de inducción electromagnética generados por un circuito sobre sí mismo llamados de inducción propia o autoinducción; y los producidos por la proximidad de dos circuitos llamados de inductancia mutua.

Un ejemplo de inductancia propia, lo tenemos cuando por una bobina circula una corriente alterna. Como sabemos, al circular la corriente por la bobina formará un campo magnético alrededor de ella, pero al variar el sentido de la corriente también lo hará el campo magnético alrededor de la bobina, con lo cual

se produce una variación en las líneas del flujo magnético a través de ella, esto producirá una fem inducida en la bobina.

La fem inducida con sus respectivas corrientes inducidas son contrarias a la fem y la corriente recibidas. A este fenómeno se le llama autoinducción.

Por definición: la autoinducción es la producción de una fem en un circuito por la variación de la corriente en ese circuito. La fem inducida siempre se opone al cambio de corriente. La capacidad de una bobina de producir una fem autoinducida se mide con una magnitud llamada inductancia. La bobina es conocida como autoinductor o simplemente inductor. En muchos circuitos de corriente alterna se utilizan inductores o bobinas con el objetivo de producir, en forma deliberada, inductancia en el circuito; cuando ésta

posee un gran número de espiras tiene un alto valor de inductancia y en caso contrario su valor es pequeño. Cuanto mayor sea la inductancia, más lentamente se elevará o descenderá la corriente dentro de la bobina.

La unidad de inductancia es el Henry (H), llamada así en honor de Joseph Henry (1797-1878), maestro y físico estadounidense pionero en el estudio del electromagnetismo.

Como el fenómeno de la inductancia se debe a que un cambio de corriente en una bobina induce una fem en ella, el Henry se puede definir en términos de la fem inducida por unidad de rapidez de cambio de la corriente.

CALCULO DE LA INDUCTANCIA

La inductancia aproximada de una bobina de una sola capa bobinada al aire puede ser calculada con la fórmula* simplificada:

L (microH)=d².n²/18d+40 l

Donde:

L = inductancia en microhenrios
d = diámetro de la bobina en pulgadas
l= longitud de la bobina en pulgadas
n = número de espiras

La notación se explica en la figura 1.

* Para poder utilizar esta fórmula con las medidas en centímetros, debe multiplicarse el segundo miembro por el factor 0,394. Así

L (microH)=0,394.(d².n²/18d+40 l)

Esta fórmula es una buena aproximación para bobinas que tengan una longitud igual o mayor que 0,4 d.

Ejemplo: Suponga una bobina que tiene 48 espiras bobinadas a razón de 32 espiras por pulgada y un diámetro de 314 de pulgada. Por tanto, d = 0,75 l = 48/32 = 1,5 y n = 48. Sustituyendo:

L = 0,75² x 48² / (18 x 0,75) + (40 x 1,5) = 1.296 / 73,5 = 17,6 microH

Para calcular el número de espiras requeridas en una bobina de una sola capa para obtener una determinada inductancia:

n= raiz cuadrada de( L ( 18d + 40l ) / d

EJEMPLO 1

Suponga que se requiere una inductancia de 10 microH.

La forma en que se va a bobinar la bobina tiene un diámetro de 1 pulgada y longitud suficiente para acomodar una bobina de 1- 1/4 de pulgada de largo.

Por tanto:

d = 1

l = 1,25

L = 10 microH.

Sustituyendo:

n=raiz cuadrada de ( 10. ( (18x1 ) + (40 x 1,25) ) ) / 1

n=raiz cuadrada de 680= 26,1 espiras

Una bobina de 26 espiras estaría lo suficientemente próxima a efectos prácticos. Puesto que la bobina tendrá 1,25 pulgadas de longitud, el número de espiras por pulgada será de 26,1/1,25 = 20,9. Consultando la tabla de hilos,encontramos que un hilo del numero 17 esmaltado (o cualquiera menor) es válido. Se obtiene la inductancia adecuada bobinando el número de espiras requeridas sobre la forma y ajustando la separación entre espiras hasta que se obtiene un espaciado uniforme con una longitud de 1,25 pulgadas.

ENLACES DE FLUJO

Con ayuda de las líneas de fuerza vamos a desarrollar el concepto de flujo del campo eléctrico y establecer un teorema de gran utilidad conocido como teorema de Gauss, que permitirá obtener la expresión del campo magnético en distribuciones de carga con un alto grado de simetría. En el apartado anterior establecimos que la densidad de líneas de fuerza era proporcional a la intensidad del campo eléctrico en esa zona. Podemos definir una magnitud relacionada con la densidad de líneas de fuerza y establecer su valor cuantitativamente. Si consideramos una determinada superficie S perpendicular al campo E, definimos el flujo del campo eléctrico como el producto del módulo del campo por el área de la superficie:

Como el campo es proporcional al número de líneas de fuerza por unidad de área, el flujo eléctrico es proporcional al número de líneas de fuerza que atraviesan la superficie.

A fin de poder generalizar y poder considerar superficies que no sean perpendiculares en todos los puntos al campo, la definición más correcta del flujo es la siguiente:

siendo n un vector unitario perpendicular a la superficie en cada punto. De este modo solamente se considera en cada punto de la superficie la componente del campo eléctrico que es perpendicular a la misma.

Finalmente, y para tener en cuenta tanto la posible curvatura de la superficie como los distintos valores que puede tomar el módulo del campo eléctrico en los distintos puntos de la superficie, la definición correcta del flujo del campo eléctrico vendrá dada como una suma integral de los distintos elementos diferenciales que componen la superficie:

[1.22]

A menudo nos interesará conocer el flujo del campo eléctrico a través de una superficie cerrada, con lo cual la suma se extenderá a toda una superficie cerrada, y el vector nunitario debe ser normal y exterior a la superficie

de esta manera se cuenta la cantidad de líneas de fuerza que salen de la superficie cerrada S menos la cantidad de líneas de fuerza que entran en ella.

Por ejemplo, si consideramos una carga puntual q y una superfie esférica de radio a centrada en ella, el flujo del campo eléctrico a través de esta superficie valdrá, teniendo en cuenta.

Se ha tenido en cuenta que tanto el campo eléctrico como el vector unitario normal a la superficie son paralelos, ambos en la dirección radial y dirigidos hacia fuera. Además el módulo del campo eléctrico puede salir fuera de la integral, dado que depende exclusivamente de la distancia a la carga, y en toda la superficie esférica la distancia es constante e igual al radio. Por lo tanto en este caso el flujo del campo eléctrico es el producto del módulo del campo por el área de la superficie esférica de radio a. La última igualdad la hemos podido expresar porque el flujo a través de una superficie cerrada era igual al número neto de líneas de fuerza que salía de la misma, y porque el número de líneas de fuerza que abandona una carga es proporcional al valor de la carga. Pero además, con el ejemplo de la carga puntual podemos conocer la constante de proporcionalidad. De acuerdo con [1.9], que nos daba la expresión del campo debido a una carga puntual, si la particularizamos para la superficie esférica de radio a obtenemos.

Este resultado que se ha obtenido para una carga puntual es válido para cualquier distribución de cargas. Se puede enunciar diciendo que el flujo del campo eléctrico a través de una superficie cerrada es igual a la carga que encierra dicha superficie dividido por e ₀. Esta afirmación se denomina Ley de Gauss, y se expresa matemáticamente de la siguiente manera:

ENERGIA ASOCIADA AL CAMPO MAGNETICO

La energía almacenada por un inductor puede expresarse por unidad de volumen, lo que nos da el concepto de densidad de energía en el campo magnético, que es un concepto similar al de densidad de energía en el campo eléctrico visto anteriormente. Por simplicidad considere un solenoide cuya inductancia está dada por la ecuación.
L= μoN²A
l

El campo magnético de un solenoide está dado por la ecuación B=μoNI. Despejando I de esta ecuación obtenemos: I= B
μoN
En general queda de la siguiente forma:
UB=1/2LI²=1/2μoN²A/l(B/μoN)²=(B²/2μo)(AL)
Debido a que AL es el volumen del solenoide, la energía almacenada por unidad de volumen en un campo magnético es la siguiente:
U_^B=UB = B².
AL 2μo

Donde:
U^B= Densidad de energía magnética asociada a un inductor.
UB = Energía almacenada en un inductor.
B = Campo magnético.
μo= Constante de permeabilidad del aire 12.56 x10^-7 Tm/A.

DENSIDAD DE ENERGIA MAGNETICA

Ya que Al es el volumen del selenoide, la energía almacenada por unidad de volumen en un campo magnético está dada por

Aunque la ecuación anterior se dedujo para el caso específico de un soleniode, ésta es valida pora cualquier región del espacio en donde exista un campo magnético. Obsérvese que es similar en forma a la ecuación de la energía por unidad de volumen almacenada por un campo eléctrico. En ambos casos la densidad de energía es proporcional al cuadrado de la intensidad del campo.

INDUCTANCIA MUTUA

Como se verá a continuación, la inductancia (mutua y autoinductacia) es una característica de los circuitos que depende de la geometría de los mismos. Sean dos circuitos arbitrarios descritos por las curva

γ 1

γ 2

por donde circulan corrientes

I 1

I 2

, respectivamente. De ahora en más el subíndice 1 representa magnitudes correspondientes circuito 1 y análogamente para el circuito 2. En virtud de la Ley de Faraday se tiene

$\vec\nabla\times\vec E(\vec x_1)=-\frac{\partial\vec B(\vec x_1)}{\partial t}$ donde $\vec E(\vec x_1)$ es el campo eléctrico y $\vec B(\vec x_1)$ es el campo magnético en el circuito 1. Si ahora se toma el flujo a través del área encerrada

S 1

por el circuito 1,

$\int_{S_1}\vec\nabla\times\vec E(\vec x_1)\cdot\vec{da_1}=-\int_{S_1}\frac{\partial\vec B(\vec x_1)}{\partial t}\cdot\vec{da_1}$ y usando el Teorema de Stokes para la integral del lado izquierdo se obtiene la fem

ε 1

para el circuito 1:

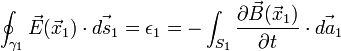
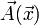$\oint_{\gamma_1}\vec E(\vec x_1)\cdot\vec{ds_1}=\epsilon_1=-\int_{S_1}\frac{\partial\vec B(\vec x_1)}{\partial t}\cdot\vec{da_1}$   Es conveniente usar que $\vec B(\vec x_1)=\vec\nabla\times\vec A(\vec x_1)$ , donde $\vec A(\vec x)$ es el potencial vectorial para reescribir lo anterior como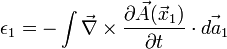

$\epsilon_1=-\int\vec\nabla\times\frac{\partial\vec A(\vec x_1)}{\partial t}\cdot\vec{da_1}$   En este punto se debe hacer una simplificación: se supondrá que el circuito no cambia en el tiempo, con lo cual la derivada parcial puede salir fuera de la integral. Esto permite entonces aplicar nuevamente el Teorema de Stokes. Matemáticamente:

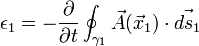
$\epsilon_1=-\frac{\partial}{\partial t}\int_{S_1}\vec\nabla\times\vec A(\vec x_1)\cdot\vec{da_1}$     $\epsilon_1=-\frac{\partial}{\partial t}\oint_{\gamma_1}\vec A(\vec x_1)\cdot\vec{ds_1}$    Dado que $\vec A(\vec x)=\frac{1}{4\pi\epsilon_0c^2}\int_V\frac{\vec J(\vec x')}{|\vec x-\vec x'|}d^3x'$ en el gauge 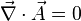$\vec\nabla\cdot\vec A=0$ donde $\vec J(\vec x)$ es la densidad de corriente que genera el campo magnético $\vec B$ . 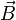En este caso la densidad de corriente corresponde a la del

circuito 2, por lo que $\vec A(\vec x_1)=\frac{1}{4\pi\epsilon_0c^2}\int_V\frac{\vec J(\vec x_2)}{|\vec x_1-\vec x_2|}d^3x_2$ . En caso que la densidad de corriente corresponda a una curva y no a un volumen en el espacio es lícito reescribir el potencial vectorial como

$\vec A(\vec x_1)=\frac{1}{4\pi\epsilon_0c^2}\oint_{\gamma_2}\frac{I_2}{|\vec x_1-\vec x_2|}\vec{ds_2}$ . Luego, reemplazando esta última igualdad en la expresión anterior se tiene

$\epsilon_1=-\frac{\partial}{\partial t}\oint_{\gamma_1}\frac{1}{4\pi\epsilon_0c^2}\oint_{\gamma_2}\frac{I_2}{|\vec x_1-\vec x_2|}\vec{ds_2}\cdot\vec{ds_1}$   Dado que se ha supuesto que los circuitos no se modifican en el tiempo sólo

I 2

se ve afectada por la derivada temporal, con lo que

$\epsilon_1=-\frac{1}{4\pi\epsilon_0c^2}\oint_{\gamma_1}\oint_{\gamma_2}\frac{\vec{ds_2}\cdot\vec{ds_1}}{|\vec x_1-\vec x_2|}\frac{\partial I_2}{\partial t}$ El anterior razonamiento se puede repetir para el circuito 2 dando como resultado

$\epsilon_2=-\frac{1}{4\pi\epsilon_0c^2}\oint_{\gamma_2}\oint_{\gamma_1}\frac{\vec{ds_1}\cdot\vec{ds_2}}{|\vec x_2-\vec x_1|}\frac{\partial I_1}{\partial t}$ Claramente las constantes que acompañan a las derivadas temporales en ambos casos son coeficientes que sólo dependen de la geometría de los circuitos y además son iguales. Luego se llama inductancia mutua,

M

a dicha constante

$M=-\frac{1}{4\pi\epsilon_0c^2}\oint_{\gamma_1}\oint_{\gamma_2}\frac{\vec{ds_2}\cdot\vec{ds_1}}{|\vec x_1-\vec x_2|}$

INTRODUCCION

Desde el siglo VI a. C. ya se conocía que el óxido ferroso-férrico, al que los antiguos llamaron magnetita, poseía la propiedad de atraer partículas de hierro. Hoy en día la magnetita se conoce como imán natural y a la propiedad que tiene de atraer los metales se le denomina “magnetismo”.

Los chinos fueron los primeros en descubrir que cuando se le permitía a un trozo de magnetita girar libremente, ésta señalaba siempre a una misma dirección; sin embargo, hasta mucho tiempo después esa característica no se aprovechó como medio de orientación. Los primeros que le dieron uso práctico a la magnetita en función de brújula para orientarse durante la navegación fueron los árabes.

Como todos sabemos, la Tierra constituye un gigantesco imán natural; por tanto, la magnetita o cualquier otro tipo de imán o elemento magnético que gire libremente sobre un plano paralelo a su superficie, tal como lo hace una brújula, apuntará siempre al polo norte magnético. Como aclaración hay que diferenciar el polo norte magnético de la Tierra del Polo Norte geográfico. El Polo Norte geográfico es el punto donde coinciden todos los meridianos que dividen la Tierra, al igual que ocurre con el Polo Sur.

Sin embargo, el polo norte magnético se encuentra situado a 1 200 kilómetos de distancia del norte geográfico, en las coordenadas 78º 50´ N (latitud Norte) y 104º 40´ W (longitud Oeste), aproximadamente sobre la isla Amund Ringness, lugar hacia donde apunta siempre la aguja de la brújula y no hacia el norte geográfico, como algunas personas erróneamente creen.

OBJETIVO DE LA FISICA EN ING. EN SISTEMAS COMPUTACIONALES